康信视点|根据数式修改权利要求时修改不超范围的论述

作者|纪秀凤 北京康信知识产权代理有限责任公司

（本文系知产力获得授权的稿件，转载须征得作者本人同意，并在显要位置注明文章来源。）

（本文2523字，阅读约需5分钟）

在答OA时，会遇到根据数式修改权利要求的情况。如果数式比较复杂，则修改不超范围的论述变得复杂。通过分享以下案例，希望对根据数式修改权利要求时理解数式以及论述不超范围有所帮助。

在该案例中，在答复OA1时，客户对权利要求1进行了下面的修改，并说明该修改是根据说明书第【0094】、【0099】段的记载进行的。

即，将权利要求1从

“一种相关运算方法，用于对接收码信号与复制码信号进行相关运算，其中，所述接收码信号通过对已接收定位卫星信号的接收信号进行解调而获得，所述相关运算方法的特征在于，包括：

对使码片周期的到来时间各偏移1/n码片而得到的第1至第n到来时间上的所述接收码信号的各值与码片周期中的所述复制码信号的值进行相关运算；以及

通过合成所述相关运算的结果，获得1/n码片间隔的相关运算结果，

其中，n为大于等于2的整数。”

修改为

“一种相关运算方法，用于对接收码信号与复制码信号进行相关运算，其中，所述接收码信号通过对已接收定位卫星信号的接收信号进行解调而获得，所述相关运算方法的特征在于，包括：

以1/n码片间隔对接收码信号进行采样，

对使码片周期的到来时间各偏移1/n码片而得到的第1到来时间至第n到来时间上的所述接收码信号的各值与码片周期中的所述复制码信号的值进行相关运算，从而获得第1相关运算的结果至第n相关运算的结果；以及

通过合成所述第1相关运算的结果至第n相关运算的结果，获得1/n码片间隔的第1相关运算结果，

对所述第1到来时间上的所述接收码信号的值与使码片周期的到来时间偏移1码片而得到的码片周期中的所述复制码信号的值进行相关运算，从而获得第n＋1相关运算的结果，

通过合成所述第2相关运算的结果至第n＋1相关运算的结果，获得1/n码片间隔的第2相关运算结果，

其中，n为大于等于2的整数。”

在OA2中，审查员指出“对所述第1到来时间上的所述接收码信号的值与使码片周期的到来时间偏移1码片而得到的码片周期中的所述复制码信号的值进行相关运算，从而获得第n＋1相关运算的结果，通过合成所述第2相关运算的结果至第n＋1相关运算的结果，获得1/n码片间隔的第2相关运算结果”这种修改超出了原始说明书和权利要求书记载的内容的范围。显然审查员对本申请的技术方案缺乏理解。为克服该审查意见，在答OA2时，进行了如下的意见陈述。

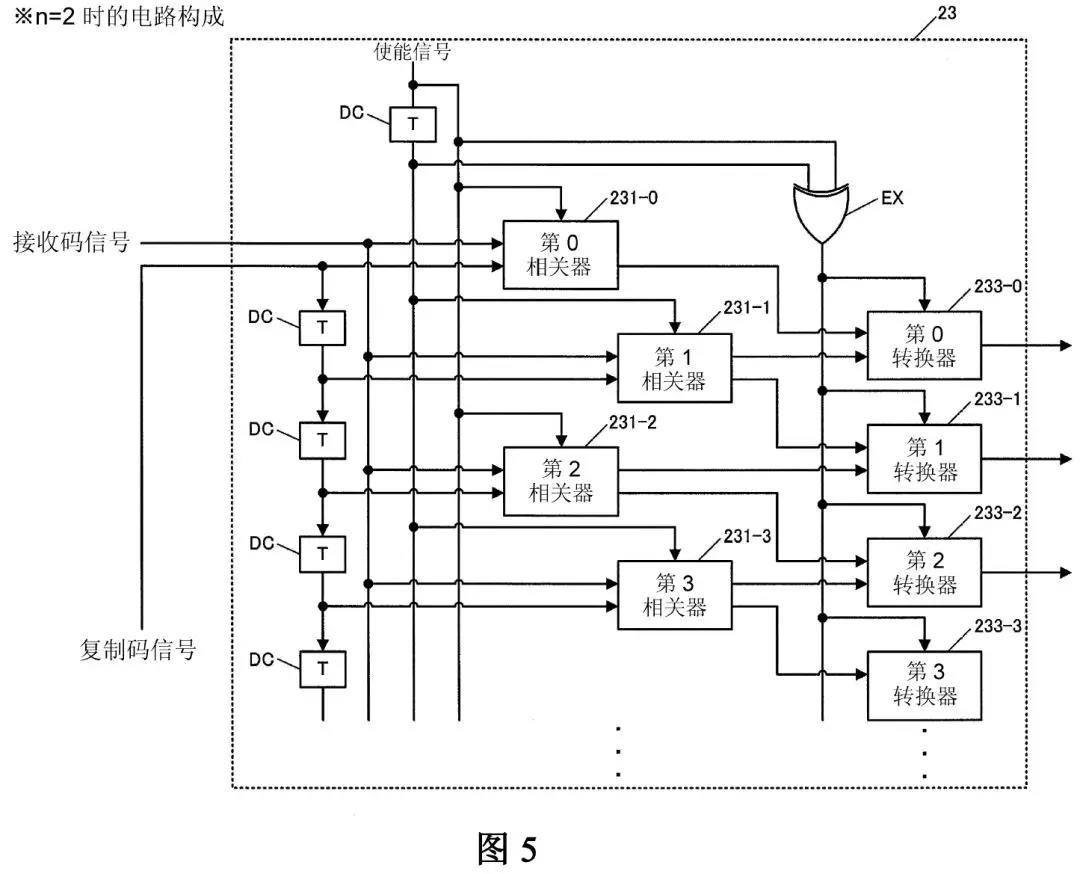
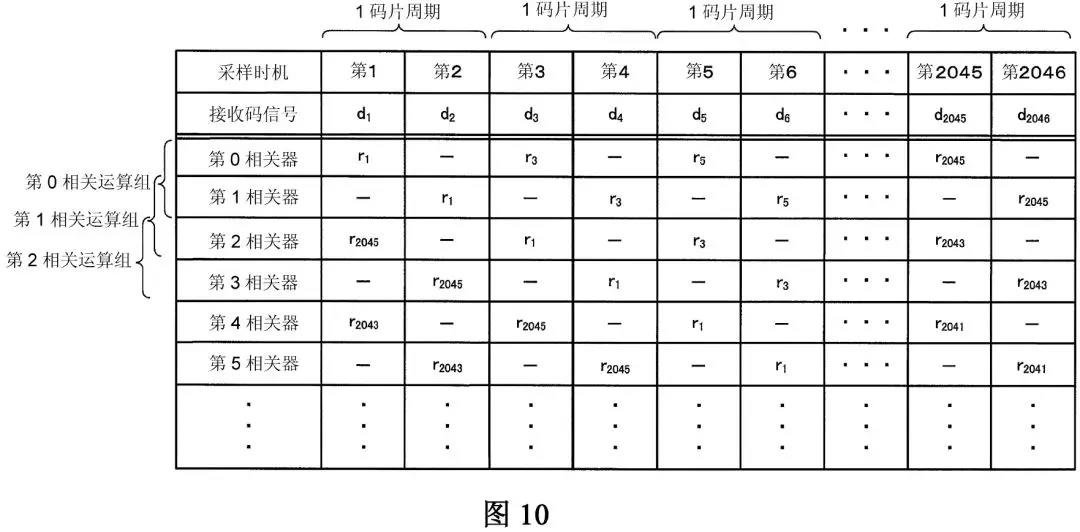
即，如果结合说明书中的数式（3）、数式（4）、说明书附图的图5（n=2时的相关运算电路部的构成图）、图10（n=2时的相关运算的时序图），来以n=2的情况进行说明（为方便理解，在下面示出在数式（4）、说明书附图的图5、10），则：

“对使码片周期的到来时间各偏移1/n（在数式（4）中，n=2）码片而得到的第1到来时间（即数式（3）中的奇数项的接收码信号、也就是数式（4）中的NewCorr0中的接收码信号的到来时间）至第n（此处n=2）到来时间（即数式（3）中的偶数项的接收码信号、也就是数式（4）中的NewCorr1中的接收码信号的到来时间）上的所述接收码信号的各值与码片周期中的所述复制码信号的值进行相关运算，从而获得第1相关运算的结果至第n相关运算的结果（即NewCorr0和NewCorr1）；以及

通过合成所述第1相关运算的结果至第n相关运算的结果（即，合成NewCorr0和NewCorr1的结果，对应于图5中的将第0相关器和第1相关器的结果输入至第0转换器），获得1/n码片间隔的第1相关运算结果（对应于第0转换器的输出），

对所述第1到来时间上的所述接收码信号的值（数式（3）中的奇数项的接收码信号、即，数式（4）的NewCorr2中的d1、d3、……d2045）与使码片周期的到来时间偏移1码片而得到的码片周期中的所述复制码信号的值（即，NewCorr2中的r2045、r1、……r2043）进行相关运算，从而获得第n＋1相关运算的结果（即NewCorr2），

通过合成所述第2相关运算的结果至第n＋1相关运算的结果（即，合成NewCorr1和NewCorr2的结果，对应于图5中的将第1相关器和第2相关器的结果输入至第1转换器），获得1/n码片间隔的第2相关运算结果”。

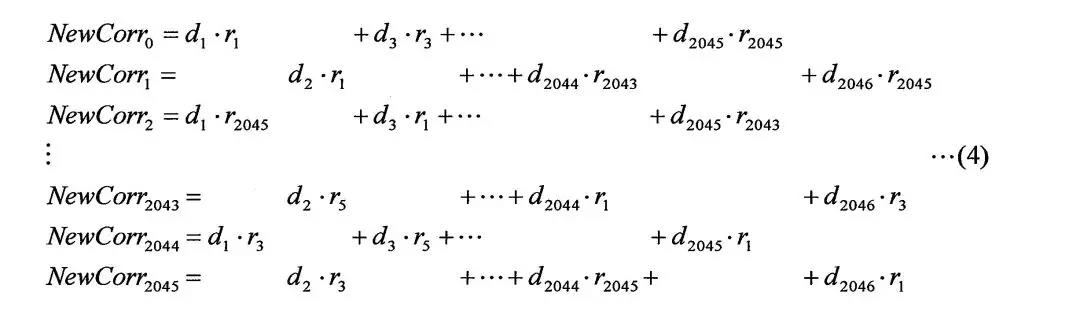
数式（4）

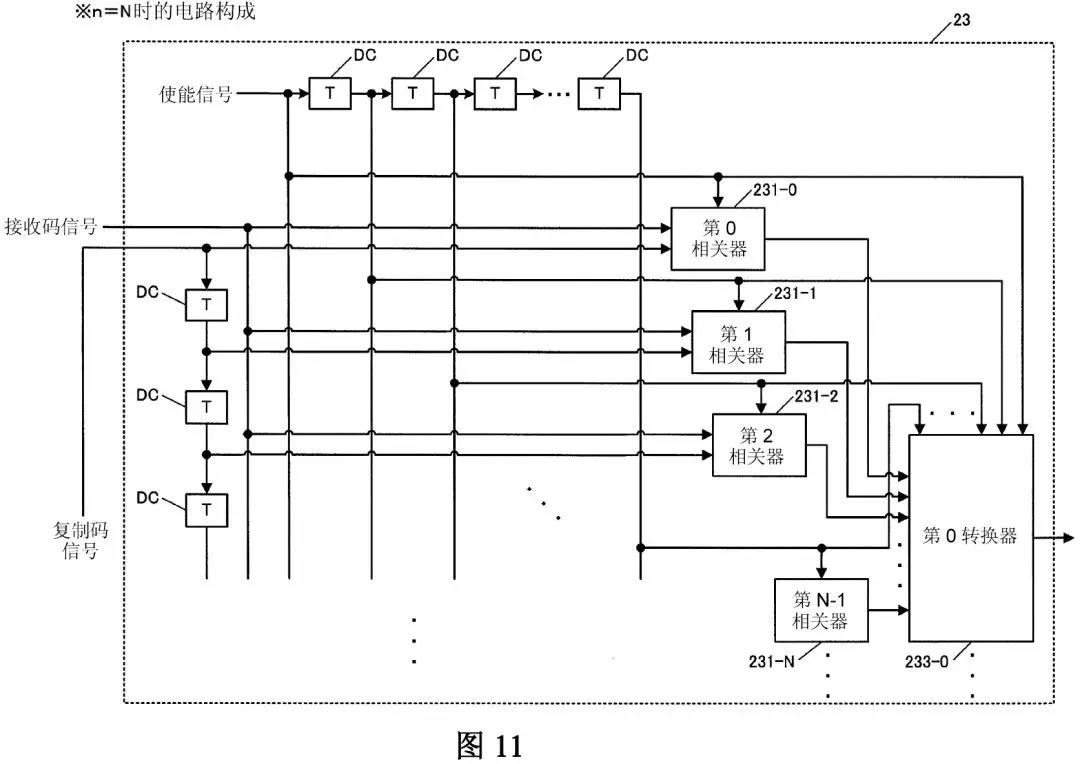
对于n=N的情况，结合说明书附图的图11（n=N时的相关运算电路部的构成图）、图12（n=N时的相关运算的时序图）（为方便理解，在下面示出说明书附图的图11、12），能够得到同样的相关运算方法。

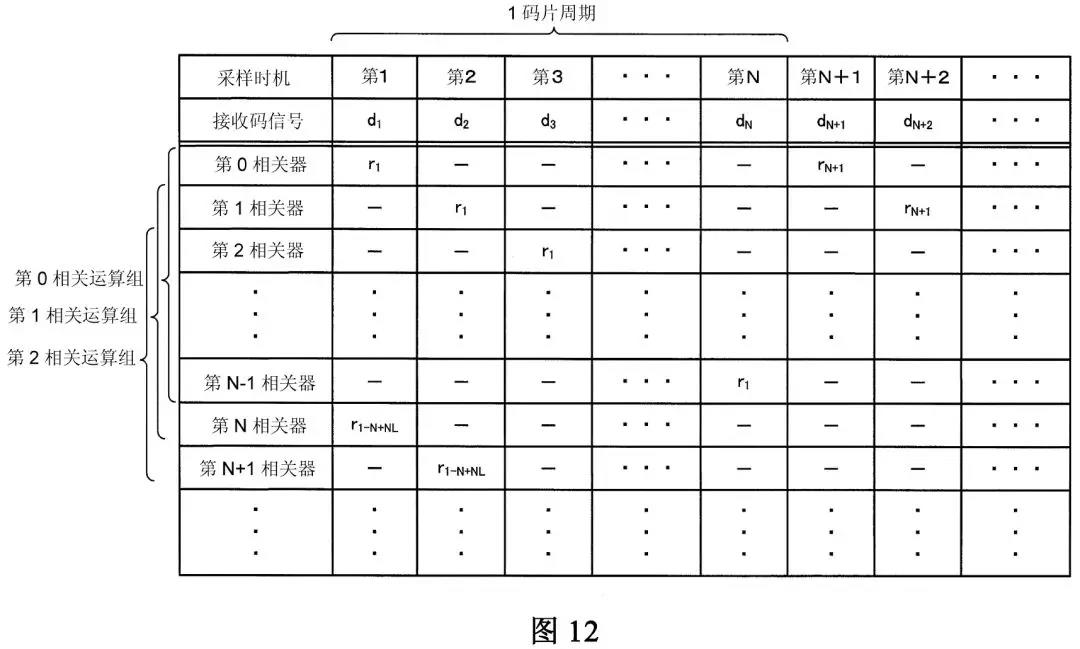
因此，权利要求1的修改没有超出原始说明书和权利要求书记载的内容的范围。

最终，该论述被审查员接受。

以上论述成功的关键，可总结为以下两点：

第一，当数式中出现表示编号的下标时，结合全文正确理解各个编号项的意义。

例如，在上述案例中，虽然在说明书中没有明确记载，但根据对说明书全文的理解，可得出在数式（4）中，第一行的d1·r1、d3·r3、…、d2045·r2045每项表示使码片周期的到来时间各偏移1/2码片而得到的各第1到来时间的相关运算的结果，第二行的d2·r1、…、d2044·r2043、d2046·r2045每项表示使码片周期的到来时间各偏移1/2码片而得到的各第2到来时间的相关运算的结果，并且，之所以最大编号是“2046”，是因为“在以CA码的1/2码片周期进行采样时，由于CA码的码长为1023码片，因此，在CA码的一个周期的相关运算中，仅是乘法就需要1023×2＝2046次运算”。

如果把n=2扩展到n=N，则可理解关于修改后的权利要求1中记载的“对使码片周期的到来时间各偏移1/n码片而得到的第1到来时间至第n到来时间上的所述接收码信号的各值与码片周期中的所述复制码信号的值进行相关运算，从而获得第1相关运算的结果至第n相关运算的结果”，第1相关运算结果包括各第1到来时间的接收码信号的值与复制码信号的值之间的乘积的总计1023项，第2相关运算结果包括各第2到来时间的接收码信号的值与复制码信号的值之间的乘积的总计1023项，…，第n相关运算结果包括各第n到来时间的接收码信号的值与复制码信号的值之间的乘积的总计1023项。

因此，达到了对权利要求1中记载的技术方案的正确理解。

第二，关注从具体到一般之间的联系。

例如，在上述案例中，结合说明书附图的图5、10、11、12，研究从图5、10记载的n=2的具体例到n=N的一般情况之间的联系，从而有助于正确理解权利要求1的技术方案。

综上所述，当根据数式修改权利要求而数式比较复杂，理解上需要花费时间时，通过正确理解数式中由各下标编号的项所代表的意义和说明书附图中从具体到一般的演绎过程，有助于有效快速地对修改不超范围的问题进行论述。

来       源：康信知识产权

联系电话：010-56571588

邮       箱：cn@kangxin.com

网       址：www.kangxin.com